
👋 들어가기 전

대학교 때 수강신청을 하지 않은 과목 중 가장 후회되는 과목이 바로 컴퓨터 그래픽스다.
행렬과 친하지 않았고 내가 UI 관련 개발로 나간다고 예상하지 못했다.
좋아하는 개그맨인 박명수님이 말했던가.. "늦었다고 생각했을 때가 진짜 늦었다.. "
평생을 관통하는 말인 것 같다.

그렇다고 포기는 할 수 없으니 .. 컴퓨터 그래픽스 관련 내용을 접하게되면 피하지는 말아보자.
이번 포스팅은 컴그에서 기본적인 선형 변환으로 먼저 시작해보자.
✊ 변환이란
선형 변환에서 먼저 변환의 의미부터 생각해보자.
가장 간단한 예는 바로 함수이다
우리는 프로그래밍에서 함수를 어떻게 이용하고 있을까?
Input이 함수를 거쳐 output으로 변환 된다.
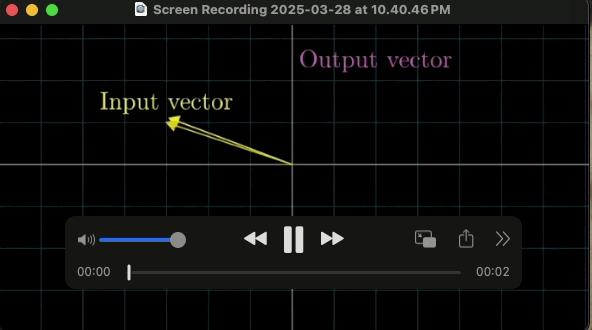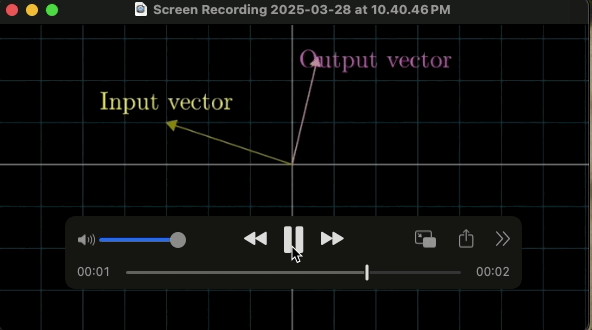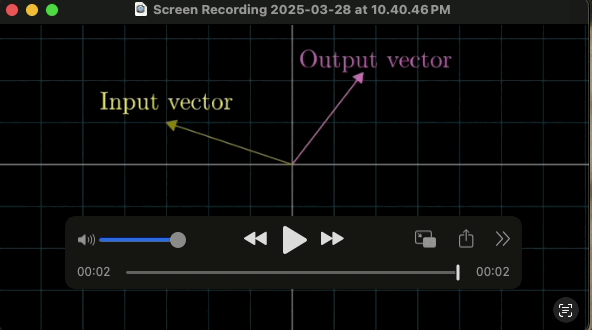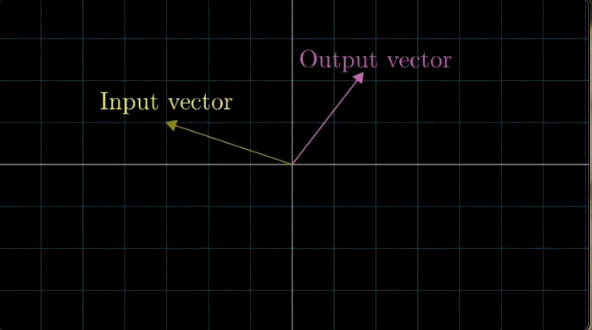
마찬가지로 입력 벡터가 변환을 통해 출력 벡터가 나오는게 변환이다.
출력 벡터로 변환하는 방법은 크게 2가지가 있다.
첫번 째 화살표를 옮기는 방법이 있고
두번 째는 좌표계, 즉 공간 자체를 움직이는 것이다.
우리는 단일 벡터를 움직이는 것에서 멈추지 않고 공간 자체를 변환하는 것을 변환이라고 정의한다.
☝️선형 변환
정의
위에서 우리는 변환이라는 단어의 정의를 살펴봤다
선형 변환이란 모든 격자선이 평행하고 균일한 간격을 유지하는 변환을 의미한다.
기하학적 해석
다음 두식을 만족하면 변환 T는 선형 변환이라고 부른다.

1) 변환 후 벡터 = 두개의 벡터의 합으로 표현될 수 있다.
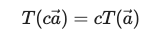
2) 변환 후 벡터 = 두개의 벡터의 합으로 표현될 수 있다.
정리하면, 변환 후 벡터는 새로운 기저벡터의 배의 합으로 표현될 수 있다.
✌️ 행렬은 선형 변환이다.
학습을 하기위해 여러 블로그를 돌아디닐 때 이 문구가 가장 많이 보였다.
왜 그럴까 ??
먼저 행렬의 곱으로 표현하면 다음과 같다.
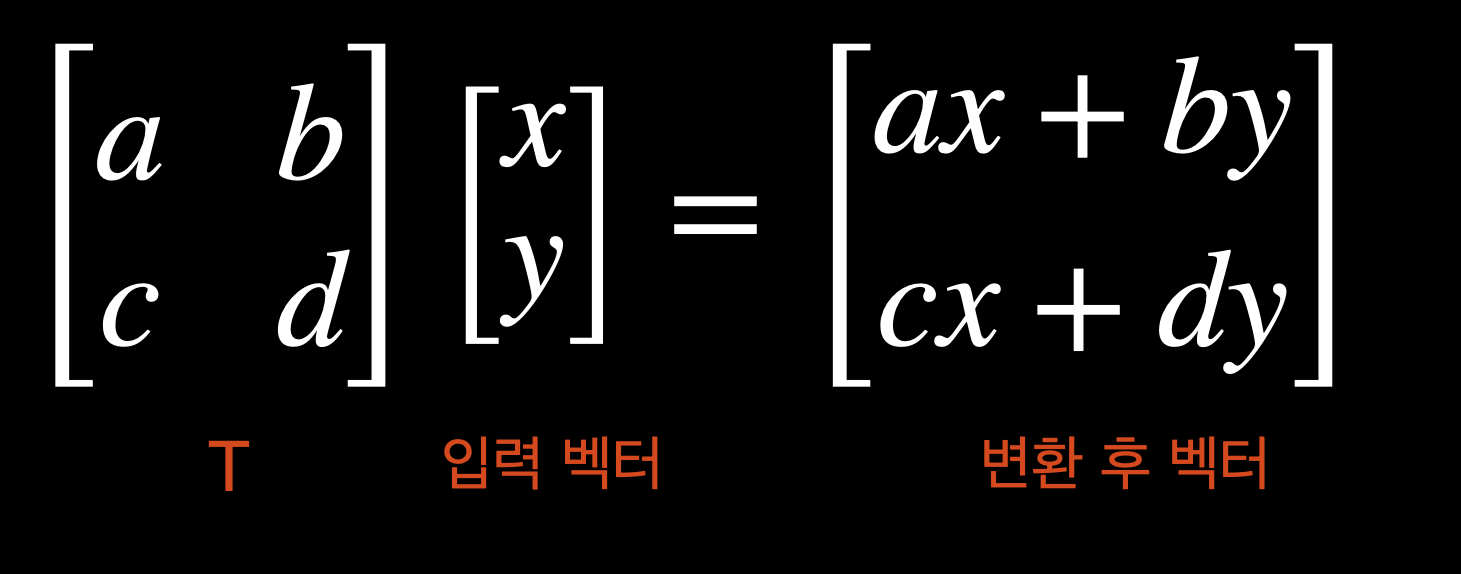
변환 T(2x2) 형렬을 통해 입력백터 (x,y)를 변환 후 벡터를 얻었다.
이거를 다음과 같이 쪼개면 어떻게 해석할 수 있을까??

변환 T배열을 2개의 기저벡터로 쪼갠 후, 입력 벡터를 상수로 이용한다.
위에 선형 변환의 기하학적 해석인 새로운 기저벡터의 배의 합으로 표현이 가능하다.
(배의 합은 여기서 x배, y배를 의미)
👍 선형 변환의 예시
↗️ shearing (밀림, 전단 변환)
정의
한 축을 따라 밀리는 변환
변환의 결과는 위에서 살펴본 것 처름 (ax+by, cx + dy)이다.
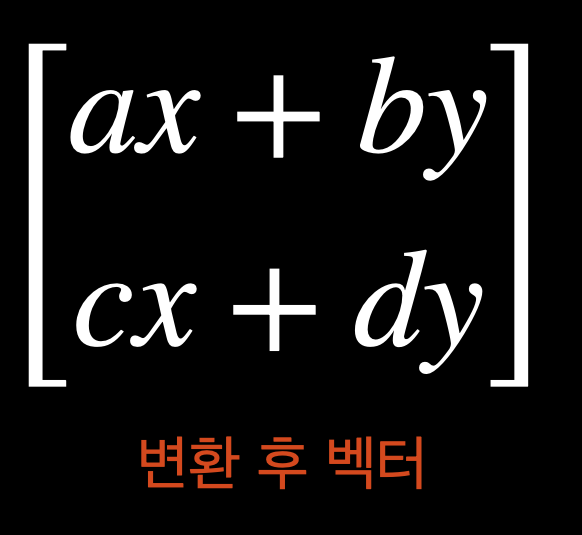
해석을 해보면 다음과 같다. 첫번째 축 ax+by 만큼 밀리고 두번 째축은 cx+dy 만큼 밀린다.
실졔 예를 보면 조금 더 이해가 빠르게 된다.

변환 T가 a = 2, b = 1 , c = 1 , d = 2이면 첫번째 축은 x축을 기점으로 2배 밀리고 y축 기점으로 1배 밀린다.
마찬가지로 두번 째 축은 x축으로 1배, y축으로 2배 만큼 밀린다.
결과화면의 빨간 화살 벡터와 초록색 벡터의 늘어나는 변화율을 살펴보면 편한다.

🔄 rotation(회전)
정의
θ 회전할 때 사용한다, 이 때 우리가 아는 데카르트 좌표계 기준 반시계 방향으로 회전한다.
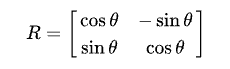
θ = π/2 일때를 보면 정확히 반시계 방향으로 90° 회전한다.

😀 소감 및 마무리
선형 변환에는 permutation, projection 등 많은 변환이 있지만 ...
필요에 의해서 적는 것이 현재 블로그 포스팅의 철칙이기 때문에
해당 변환이 필요하면 이어서 적어보자.

다음 포스팅은 드디어 최종목표인 아핀 변환에 대해 알아보자.
출처
https://angeloyeo.github.io/2019/07/15/Matrix_as_Linear_Transformation.html
행렬과 선형변환 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
https://blog.naver.com/songsite123/223319658381
선형 변환(Linear transformation)
오늘 포스팅의 이미지/GIF는 모두 3Blue1Brown의 Essence of linear algebra 에서 가져왔습니다. 시...
blog.naver.com
https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
Essence of linear algebra
A free course offering the core concept of linear algebra with a visuals-first approach.
www.youtube.com
'CS > 이론' 카테고리의 다른 글
| clang과 LLVM에 관하여 (0) | 2025.12.13 |
|---|---|
| Throttle vs Debonuce (4) | 2025.08.06 |
| [Text 시리즈 1] Typographical Concepts (2) | 2025.07.17 |
| OAS(Open API Specification) (1) | 2025.07.04 |
| 아핀 변환(Affine Transformation) (0) | 2025.03.30 |