
👋 들어가기 전

우리는 이전 시간에 선형 변환을 간단하게 학습했다.
사실 최종 목적지는 아핀 변환을 학습하기 위한 빌드업!
iOS 개발을 하다보면 특히, 보기 좋은 효과를 위해 알게 모르게 사용했던 AffineTransform 객체가 있다.
AffineTransform | Apple Developer Documentation
A graphics coordinate transformation.
developer.apple.com
여기에 깔려있는 기본적인 이론을 오늘 정리하고 해당 객체는 iOS 카테고리로 다시 정리해보자.
✊homogenous coordinates(동차 좌표)
먼저 Homogeneous 좌표계를 먼저 알아보자.

Homogeneous 좌표계는 위에 2가지 조건으로 설명이 가능하다.
1) (x,y)와 (wx,wy,w)은 동등하다.
2) w은 0이 아닌 상수이다.
정리하면 특정 좌표에 대한 상수 스케일의은 무시된다는 의미를 가진다.
간단히 살펴보자. w가 1이라고 한다면
(x,y) 는 (x,y,1) equiv한다라는 뜻인데
(x,y)는 2차원 좌표고 (x,y,1)는 엄연히 3차원 좌표인데 동등하다 ??

위 사진에서 L위에 있는 모든 점은 동등한 점들이다.
여기서 z값이 1이면 2D(사실상 3D긴함) , z값이 1 이상이 되면 3D로 변하는데
Homogeneous 좌표계에서는 모두 동등하게 보기 때문에 두 차원간의 좌표 변환이 매우 간편해진다.
3차원이 될 때는 w를 곱해주면되고 , 2차원일 때는 w로 나눠주면된다.
조금 뜬금없지만 정리하면 homogeneous 좌표계를 사용하면 affine 변환을
하나의 단일(single) 행렬로 표현할 수 있다.
이 말의 의미는 밑에서 자세히 설명할테니 일단 문구만 기억 해보자.
☝️아핀 공간
아핀 공간이 없다면
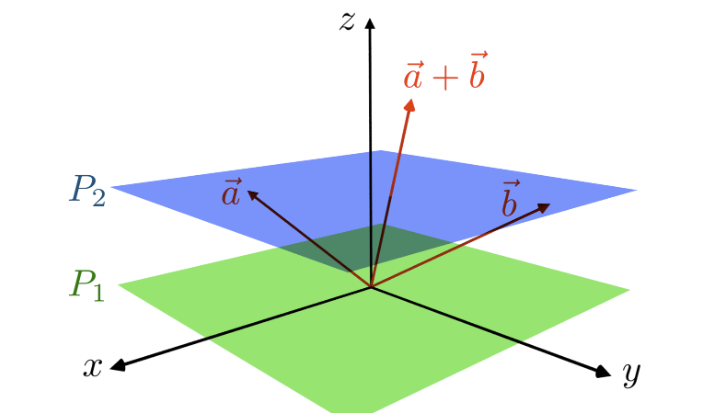
벡터는 크기(화살표의 길이)와 방향을 가지고 있는 개념이다.
여기서 중요한 점은 시작위치가 어디 있던, 방향과 크기가 같으면 같은 벡터로 취급되는 문제가 있다.
등장
이런 문제를 해결하기위해 고안된 공간이 바로 아핀 공간이다.
아핀 공간은 위에서 설명한 벡터의 특징에 바로 위치라는 변수를 추가한 공간이다.
정리하면 기존 벡터(크기와 방향)공간 + 위치 = 아핀 공간이 된다.
이동 변환
임의의 벡터(x,y)를 지정한 (a,b)만큼 이동시킬 때는 행렬의 덤셈 행태로 표현된다.

✌️아핀 변환
정의
유쿨리드 기하학에서, 아핀 변환은 선과 평행성을 보존하는 기하 변환이다.
여기서 거리와 각은 보존되지 않을 수 있다.
아핀 변환은 선형 변환과 평행이동의 합이다.
이전에 학습했던 선형 변환을 살펴보면 많은 변환이 있지만
항상 보존되는게 바로 원점이다.
위에서 아핀 공간은 보면 위치라는 변수가 벡터 공간에 추가됐다는 것을 보면
아핀 변환에서는 원점이 보존되지 않아도 된다는 것을 간접적으로 느낄 수 있다.
원점을 변환한다는 것은 이동이 된다는 것
아핀 변환 = 선형 변환 + 평행이동
아핀 변환은 선형 변환이 될 수 있지만, 선형 변환은 아핀 변환이 될 수 없다
(원점을 보존해야하므로 이동 x)
행렬 표현
아핀 변화는 다음과 같은 형태이다 .

여기서 빨간 부분만 집중하면, 어디서 봤던 형태인데 ??


바로 이전 시간에 봤던 선형 변환의 T 부분이 있다.
그러면 새로운 값은 두 부분이 있다.

주황색 부분과 초록색 부분으로 나눌 수 있는데
주황색 부분은 다음을 의미한다.
- tx = x 방향 평행이동
- ty = y 방향 평행이동
마지막 초록색 부분은 마지막 챕터에서 설명해보자.
먼저 예제와 함께 살펴보자.
예제

주워진 파라미터는 a = 2 , b = 0 , c = 0 , d = 2, tx = 3, ty = 4
이후 결과 벡터 V'를 보면 입력 벡터 기준
- x는 2배 확대 이후 x축으로 3만큼 평행이동
- y는 2배 호가대 이후 y축으로 4만큼 평행이동
변환에 대한 파라미터 형식
a ,b,c,d 의 값을 통해 선형 변환인, scale, rotatin, shearing이 결정되고 tx,ty 값을 통해
평행 이동이 정해진다.
❓마지막 행이 0 0 1인 이유
위에서 마지막 초록색 부분에 대한 설명을 이어나가보자.
이 개념을 설명하기 위해서는 가장 처음에 학습한 homogenous coordinates(등차 좌표) 개념이 필요하다.
2D 선형 변환은 회전, 스케일, 회전등 다양한 변환이 가능하지만, 평행이동에 대한 표현을
2차원 행렬에서는 표현할 수 없었다.
하지만 아핀 변환은 = 선현 변환 + 평행이동을 합쳤기 때문에
평행 이동을 위해 차원이 하나 더 필요하다.
이때 우리는 등차 좌표에서 2차원 좌표 (x,y)은 3차원 좌표(x,y,1)과 동등하다는 것을 배웠다.
그렇기 때문에 0,0,1을 통해 x와 y는 무시되고 z값을 1로 유지해주는 동등한 효과를 받을 수 있다.
이렇게 되면 변환 후에도 점은 점으로 벡터는 벡터, 평면은 평면으로 유지될 수 있다.
😀 소감 및 마무리

주관적인 해석이 많이 들어가긴 했지만 최대한 많은 참고자료를 통해 해석해내봤다.
아래 CoreFoundation 프레임워크를 보면 우리가 배운 파라미터가 그대로 들어가 있다.
나중에 잘 써먹어보자.

최종적으로 정리를 해보자.
정리
1. homogenouse coordinates는 w배 형태로 나타낼 수 있는 한 선상에 있는
점들은 동등하다라고 표현한다.
2. 동등하다는 뜻은 상수 w를 무시할 수 있으며, 이전 차원과 다음 차원의
좌표 변환이 곱 또는 나누기로 표현이 가능하다.
3. 아핀 공간은 위치 + 크기 + 방향으로 판단한다.
4. 아핀변환은 선형 변환과 평행이동의 합이다.
5. 이 계산을 표현하기위해 행렬의 곱으로 표현하고 곱으로 표현이 가능케
해주는게 바로 homogenouse coordinates이다.
6. 그 보정 값을 마지막 행인 0,0,1이 담당한다.
출처
1.1 벡터의 정의와 표현
# Chapter 1: 벡터와 행렬 기초 ## 1.1 벡터의 개념과 표현 **벡터(vector)**란 크기와 방향을 가지고 있는 양을 나타내는 개념입니다. 이는 화살표로 표현…
wikidocs.net
https://hanseongbugi2study.tistory.com/174
[게임수학] 어파인 공간(Affine space)
어파인 공간?벡터공간에서는 벡터가 어디에 위치해 있던지 크기와 방향만 같다면 모두 같은 벡터로 취급한다. 따라서, 벡터 공간에서는 위의 여러 벡터가 엄연히 다른 벡터임에도 불구하고 같
hanseongbugi2study.tistory.com
https://www.youtube.com/watch?v=B8kMB6Hv2eI&t=311s
https://darkpgmr.tistory.com/78
[영상 Geometry #2] Homogeneous Coordinates
(3D 비전 geometry 2번째 파트 homogeneous coordinates 입니다) 2. Homogeneous Coordinates 먼저, 들어가기 앞서 http://blog.daum.net/shksjy/229 글을 읽어보기를 추천합니다. Homogeneous Coordinate에 대한 유래부터 의미, 특
darkpgmr.tistory.com
https://angeloyeo.github.io/2024/06/28/Affine_Transformation.html
아핀 변환 (Affine Transformation) - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
'CS > 이론' 카테고리의 다른 글
| clang과 LLVM에 관하여 (0) | 2025.12.13 |
|---|---|
| Throttle vs Debonuce (4) | 2025.08.06 |
| [Text 시리즈 1] Typographical Concepts (2) | 2025.07.17 |
| OAS(Open API Specification) (1) | 2025.07.04 |
| 선형 변환 (0) | 2025.03.30 |